
每周一题,代码无敌~
这次让我们回到算法本身,来探讨一下回溯算法:
组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]示例 2
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]思路
对于这道题来说,最困难的点就在于「candidates 中的数字可以无限制重复被选取」, 这个条件导致了最后结果的集合里面可以选的元素的数量不一定,直接导致了满足条件的可能性组合的数量暴增,给程序的复杂性带来了一定的挑战。
面对这种情况,我们就不得不尝试组合出各种能容纳最多元素的组合。在学习算法的过程中,可以理解到,类似面临这种 「查找最远路径」的问题,最适合的算法场景就是 「深度优先」搜索算法。
回到这个题目当中,我们想要找出所有满足条件的组合,就是要 「从长到短」、「从小到大」尝试所有相加不超过 target 的组合。而在如果遇到组合超过 target 的情况,则回到更 「短」一点的组合尝试其他可能性:
以这道题目的 示例 2 为例:
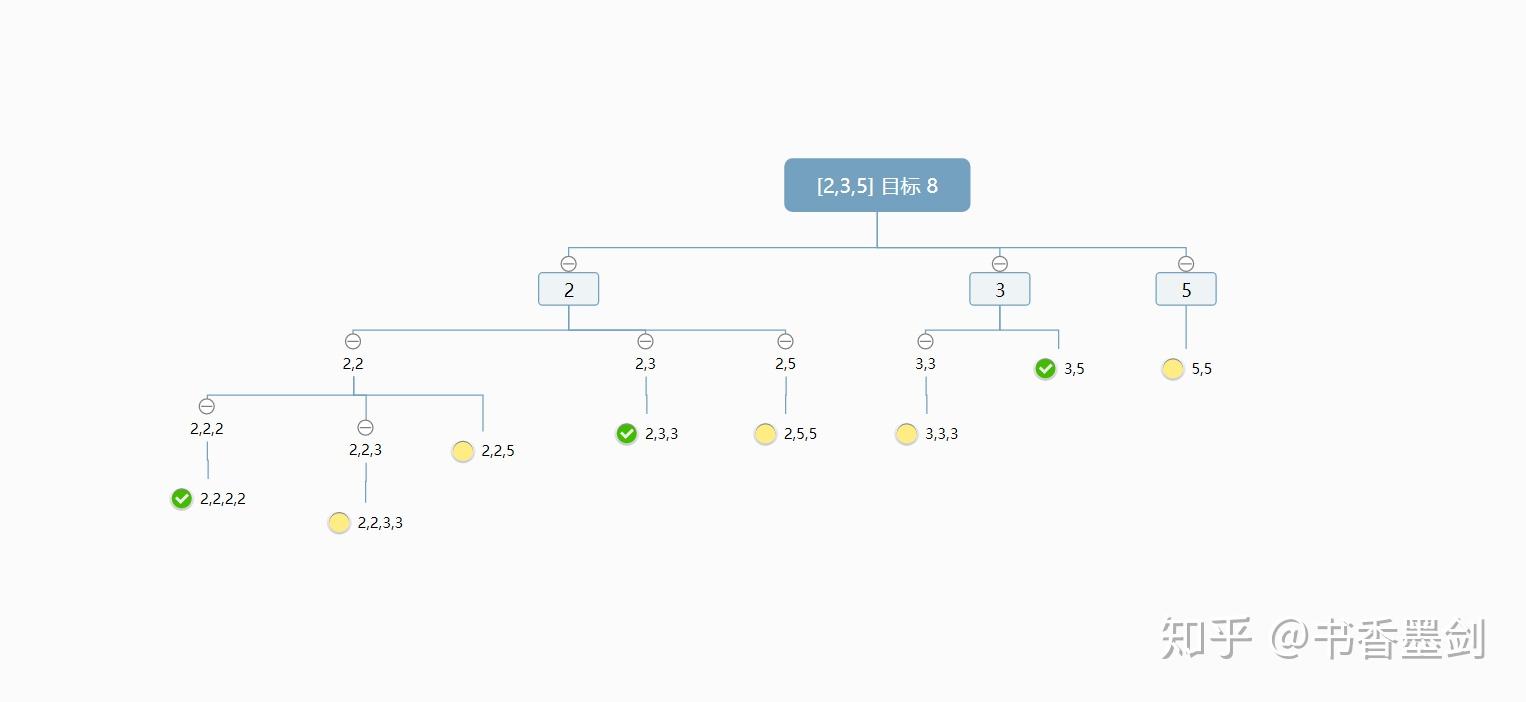
如图所示,我们从左往右,每次尝试去取到最多元素的可能性,当组合的和大于或等于 target 的时候(等于的时候要记录结果),就返回上一层,尝试新的组合(新的组合的数要比之前的大)。相当于在这里 「剪掉」了后面的可能性,并 「返回」了上一层去尝试。因此这种算法也被称为了 「回溯剪枝算法」。提一下,「回溯剪枝算法」其实就是一种 「深度优先查找」(DFS) 算法。
注意:对于这个题来说,这个算法必须在有序数组中才可以才行,因为数值越大,深度就越有限。
解法
了解了思路,我们先来看看 Helen 的解法
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
function combinationSum(candidates, target) {
const result = [];
let tmpPath = [],
start = 0;
candidates = candidates.sort((a, b) => a - b);
function backtrack(tmpPath, target, start) {
if (target === 0) {
result.push(tmpPath);
return;
}
for (let index = start; index < candidates.length; index++) {
if (target < 0) break;
tmpPath.push(candidates[index]);
backtrack(tmpPath.slice(), target - candidates[index], index);
tmpPath.pop(); //回溯
}
}
backtrack(tmpPath, target, start);
return result;
}在这里,Helen 定义了一个 backtrack 的回溯函数,在其中遍历了 candidates 数组,并在其中递归地又去回溯,从而找出所有的可能性。
注意其中 target < 0 这个条件,其实就是一个“剪枝”,把超出的可能性剪掉。只不过用了减法的形式,有点反直觉,可以多琢磨下。
而书香稍微改了下结构,把代码缩短了点:
function combinationSum(candidates, target) {
const sliceArr = candidates
.filter(item => item <= target)
.sort((a, b) => a - b),
finalArr = [];
function findCompose(target, offset, last) {
for (let i = offset; i < sliceArr.length; i++) {
const subTarget = target - sliceArr[i];
if (subTarget == 0) finalArr.push([...last, sliceArr[i]]);
if (subTarget > 0) findCompose(subTarget, i, [...last, sliceArr[i]]);
}
}
findCompose(target, 0, []);
return finalArr;
}其实差不太多,不过是因为用了 ES 6 数组的解构赋值方法,没有把每个分支都 push 进去,所以回溯的时候就可以少写一个 pop 啦~
曾大师 Go 语言时间
他在注释里顺便给我们解释了 「示例 1」,并且直接将函数命名成了 DFS(深度优先搜索)。果然很有算法大师的风范呀!
// 深度搜索加减枝,具体过程如下
// 2 -> 22 -> 222 -> 2222 -> 223(合适) -> 23 -> 233 -> 26 -> 3 -> 33 -> 333 -> 36 -> 6 -> 66 ->7(合适)
var result [][]int
var currCandidate []int
func combinationSum(candidates []int, target int) [][]int {
sort.Ints(candidates)
result=make([][]int,0)
currCandidate=make([]int,0)
DFS(target,candidates)
return result
}
func DFS(target int,candidates []int) int {
if getSum(currCandidate) == target {
temCandidate := make([]int, len(currCandidate))
copy(temCandidate, currCandidate)
result = append(result, temCandidate)
return 0
} else if getSum(currCandidate) > target {
return -1
} else { //主要看这里用0代表相同,-1代表已经超过了当前target,1则表示还能继续加
for i := 0; i < len(candidates); i++ {
currCandidate = append(currCandidate, candidates[i])
temp := DFS(target, candidates[i:])
currCandidate = currCandidate[:len(currCandidate) - 1]
if temp <= 0 {
break
}
}
}
return 1
}
func getSum(nums []int) int {
sum := 0
for i := 0; i < len(nums); i++ {
sum += nums[i]
}
return sum
}结语
OK,这样看下来,其实算法离我们也没有那么远。事实上如此,算法本身也是为了解决具体的问题而诞生的。而我们在练习的过程中,要理解到算法具体解决了什么问题,就可以在遇到类似的问题的时候迎刃而解啦~
下周见~





