【青铜三人行】每周一题@三数之和

哈喽~ 每周一题，代码无敌。欢迎各位继续观看「青铜三人行」的刷题现场。

话不多说，我们进入这周的题目吧：

三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a、b、c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如

// 给定数组
const nums = [-1, 0, 1, 2, -1, -4];

最初的解法

Helen 拿到题目，心想这道题岂不是如同上周的“两数之和”一般？无非就是多加了一个数而已。按照思路，首先暴力举出所有满足条件的三个数，再去重即可，写出了如下代码：

function threeSum(nums) {
  const results = [];
  for (i = 0; i < nums.length; i++)
    for (j = i + 1; j < nums.length; j++)
      for (k = j + 1; k < nums.length; k++)
        if (nums[i] + nums[j] + nums[k] === 0) {
          // 转换成字符串方便去重
          const strResult = [nums[i], nums[j], nums[k]]
            .sort((a, b) => a - b)
            .join(",");
          results.push(strResult);
        }
  return Array.from(new Set(results)).map(str => str.split(","));
}

拿入测试用例执行，结果正确 😎：

于是提交，结果被现实狠狠打脸……😱：

排序解法

纳尼？这道题居然有时间限制…… 太阴险了吧……😵 看样子传统的暴力破解法，在三重循环之下，时间复杂度到达了 O(n³)，时间消耗应该是远远超过了题设。

看样子想解出这道题，至少要“消灭”掉其中的一重循环。Helen 找来书香一起讨论，两人细细品味题目，发现题目要求：a + b + c == 0 ，那说明这三个在数组中的数，除开三个数都为 0 的情况，必然有正有负，有大有小。

换言之，如果给定一个“最小”的数，我们只需要在比这个数“大”的剩余数组里找出”其他”两个数，看看它们加起来的结果。如果等于 0，则加入结果，如果大于 0，则设法调整“其他两数”，使其和变小。若小于 0，则设法使“其他两数”之和变大。

而在有序数组中，调整两数相加之和的大小是只需要一次循环就可以做到的，如此一来，我们似乎就可以在 O(n²) 的时间复杂度中就可以完成题设了：

function threeSum(nums) {
  const funcSeq = (a, b) => a - b;
  const sortedNums = nums.sort(funcSeq);
  const length = sortedNums.length;
  const result = [];
  for (let i = 0; i < length; i++) {
    let num = sortedNums[i];
    let lIndex = i + 1;
    let rIndex = length - 1;
    while (lIndex < rIndex) {
      let lNum = sortedNums[lIndex];
      let rNum = sortedNums[rIndex];
      if (lNum + num + rNum === 0) {
        result.push([lNum, num, rNum].sort(funcSeq).join(","));
        rIndex -= 1;
        lIndex += 1;
      } else if (lNum + num + rNum < 0) lIndex += 1;
      else if (lNum + num + rNum > 0) rIndex -= 1;
    }
  }
  return Array.from(new Set(result)).map(str => str.split(","));
}

然而在提交时，遇到了一个诡异的测试用例，导致还是超时了 😰：

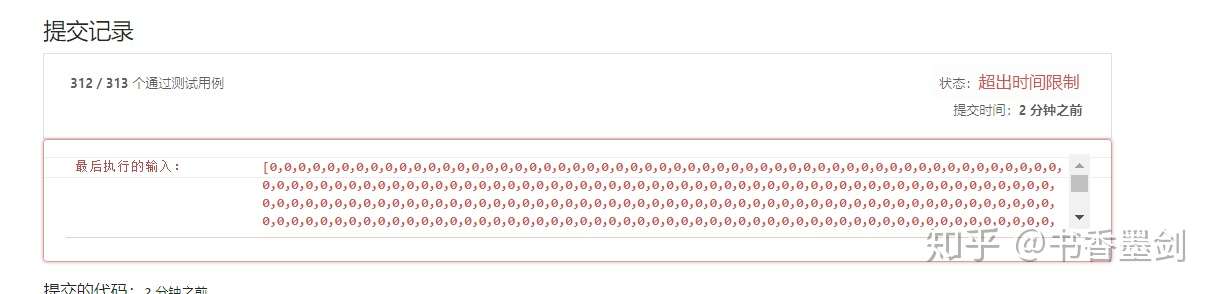
居然还有这么奇葩的测试用例！大量的 0 构成的数组。还好这并没有难倒 Helen, 既然题设里要求没有重复的三元组，那么加上了一个跳过重复元素的条件就好了：

function threeSum(nums) {
  const funcSeq = (a, b) => a - b;
  const sortedNums = nums.sort(funcSeq);
  const length = sortedNums.length;
  const result = [];
  for (let i = 0; i < length; i++) {
    let num = sortedNums[i];
    if (num === sortedNums[i - 1]) continue;
    let lIndex = i + 1;
    let rIndex = length - 1;
    while (lIndex < rIndex) {
      let lNum = sortedNums[lIndex];
      let rNum = sortedNums[rIndex];
      if (lNum + num + rNum === 0) {
        result.push([lNum, num, rNum].sort(funcSeq).join(","));
        rIndex -= 1;
        lIndex += 1;
      } else if (lNum + num + rNum < 0) lIndex += 1;
      else if (lNum + num + rNum > 0) rIndex -= 1;
    }
  }
  return Array.from(new Set(result)).map(str => str.split(","));
}

提交，代码终于顺利通过啦 😆：

优化

看到解题终于通过，大家欢欣鼓舞，也打开了更多的思路。书香发现，既然要相加等于 0，那么除开全为 0的情况，必然结果里有正有负。换言之，第一层循环选取的数字，只需要遍历“非正数”的部分就好，于是加了个条件尝试了一番：

function threeSum(nums) {
  const funcSeq = (a, b) => a - b;
  const sortedNums = nums.sort(funcSeq);
  const length = sortedNums.length;
  const result = [];
  for (let i = 0; i < length; i++) {
    let num = sortedNums[i];
    if (num > 0) break;
    if (num === sortedNums[i - 1]) continue;
    let lIndex = i + 1;
    let rIndex = length - 1;
    while (lIndex < rIndex) {
      let lNum = sortedNums[lIndex];
      let rNum = sortedNums[rIndex];
      if (lNum + num + rNum === 0) {
        result.push([lNum, num, rNum].sort(funcSeq).join(","));
        rIndex -= 1;
        lIndex += 1;
      } else if (lNum + num + rNum < 0) lIndex += 1;
      else if (lNum + num + rNum > 0) rIndex -= 1;
    }
  }
  return Array.from(new Set(result)).map(str => str.split(","));
}

而 Helen 则从“去重”这一部分上进行了优化，节省了转化成字符串，再用 Set 等数据结构去重带来的额外开销：

function threeSum(nums) {
  const funcSeq = (a, b) => a - b;
  const sortedNums = nums.sort(funcSeq);
  const length = sortedNums.length;
  const result = [];
  for (let i = 0; i < length; i++) {
    let num = sortedNums[i];
    if (num > 0) break;
    if (num === sortedNums[i - 1]) continue;
    let lIndex = i + 1,
      rIndex = length - 1;
    while (lIndex < rIndex) {
      let lNum = sortedNums[lIndex],
        rNum = sortedNums[rIndex];
      if (lNum + num + rNum === 0) {
        result.push([lNum, num, rNum]);
        while (lIndex < rIndex && sortedNums[lIndex] === sortedNums[lIndex + 1])
          lIndex++;

        while (rIndex > lIndex && sortedNums[rIndex] === sortedNums[rIndex - 1])
          rIndex--;

        (rIndex -= 1), (lIndex += 1);
      } else if (lNum + num + rNum < 0) lIndex += 1;
      else if (lNum + num + rNum > 0) rIndex -= 1;
    }
  }
  return result;
}

而优化之后的结果也是相当理想：

Extra

最后，我们照例贴上曾大师的 Go 语言代码：

func threeSum(nums []int) [][]int {

    result := [][]int{}

    var keyCountMap map[int]int /*创建集合 */
    keyCountMap = make(map[int]int, len(nums))

    for i := 0; i < len(nums); i++ {

        count, ok := keyCountMap [nums[i]]
        if ok {
            keyCountMap[nums[i]]=count+1;
        } else {
             keyCountMap[nums[i]]=1;
        }
    }

    newNums := make([]int, 0, len(keyCountMap))

    for keyi := range keyCountMap {
        newNums = append(newNums, keyi)
        if keyCountMap[keyi] > 1 {
            if keyi == 0 {
                if (keyCountMap[keyi] > 2) {
                    result = append(result, append([]int{}, 0, 0, 0))
                }
                continue
            }
            var remain = 0 - keyi * 2
            _, ok := keyCountMap [remain]
            if ok {
                result = append(result, append([]int{}, keyi, keyi, remain))
            }
        }
    }

    for i := 0; i < len(newNums); i++ {
        for j := i + 1; j < len(newNums); j++ {
            var remain = 0 - (newNums[i] + newNums[j])
            if remain == newNums[i] || remain == newNums[j] {
                continue
            }
            _, ok := keyCountMap [remain]
            if ok {
                var b1 bool = true

                for k := 0; k < len(result); k++ {
                    if (newNums[i] == result[k][0]) {
                        if (newNums[j] == result[k][1] || remain == result[k][1]) {
                            b1 = false
                            break
                        }
                    } else if newNums[j] == result[k][0] {
                        if(newNums[i] == result[k][1] || remain == result[k][1]){
                            b1 = false
                            break
                        }

                    } else if remain == result[k][0] {
                        if(newNums[i] == result[k][1] || newNums[j] == result[k][1]){
                            b1 = false
                            break
                        }
                    }
                }

                if b1 {
                    result = append(result, append([]int{}, newNums[i], newNums[j], remain))
                }
            }
        }
    }
    return result;
}

在这里，他另辟蹊径，采用了类似上周“两数之和”的题目解法，利用空间换时间，将数组转成 map 形式进行查找。同样通过了题目：

在这里，提个小问题：既然在“三数之和”可以参考“两数之和”的转换成 map 解题的方法，那在“两数之和”中，能不能参考上述“先排序，比较大小查找”的方法呢？

结尾

这周的题目难度上升为了“中等”，随着难度的上升，在解题上也无法完全做到完美。如果你有更好的思路，欢迎通过 [email protected] 邮箱联系我们~

下周见！