
先说一个消息,为了方便互相交流学习,青铜三人行建了个微信群,感兴趣的伙伴可以扫码加下面的小助手抱你入群哦!

每周一题,代码无敌~ 这次的主题是 「贪心算法」:
验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false。
示例 1
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1示例 2
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。提示
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed是popped的排列
栈结构
要做这道题,首先得了解一下什么是 「栈」。为此书香搬来了维基百科上的解释:
堆栈(英语:stack)又称为栈或堆叠,是计算机科学中的一种抽象数据类型,只允许在有序的线性数据集合的一端(称为堆栈顶端,英语:top)进行加入数据(英语:push)和移除数据(英语:pop)的运算。因而按照后进先出(LIFO, Last In First Out)的原理运作。
这个定义看起来多,其实也没什么大不了的。栈本身就是一个数组或者链表,只是人为定义它获取数据的方式只能从栈的顶端获取,因此遵循先进后出、后进先出的规则罢了。
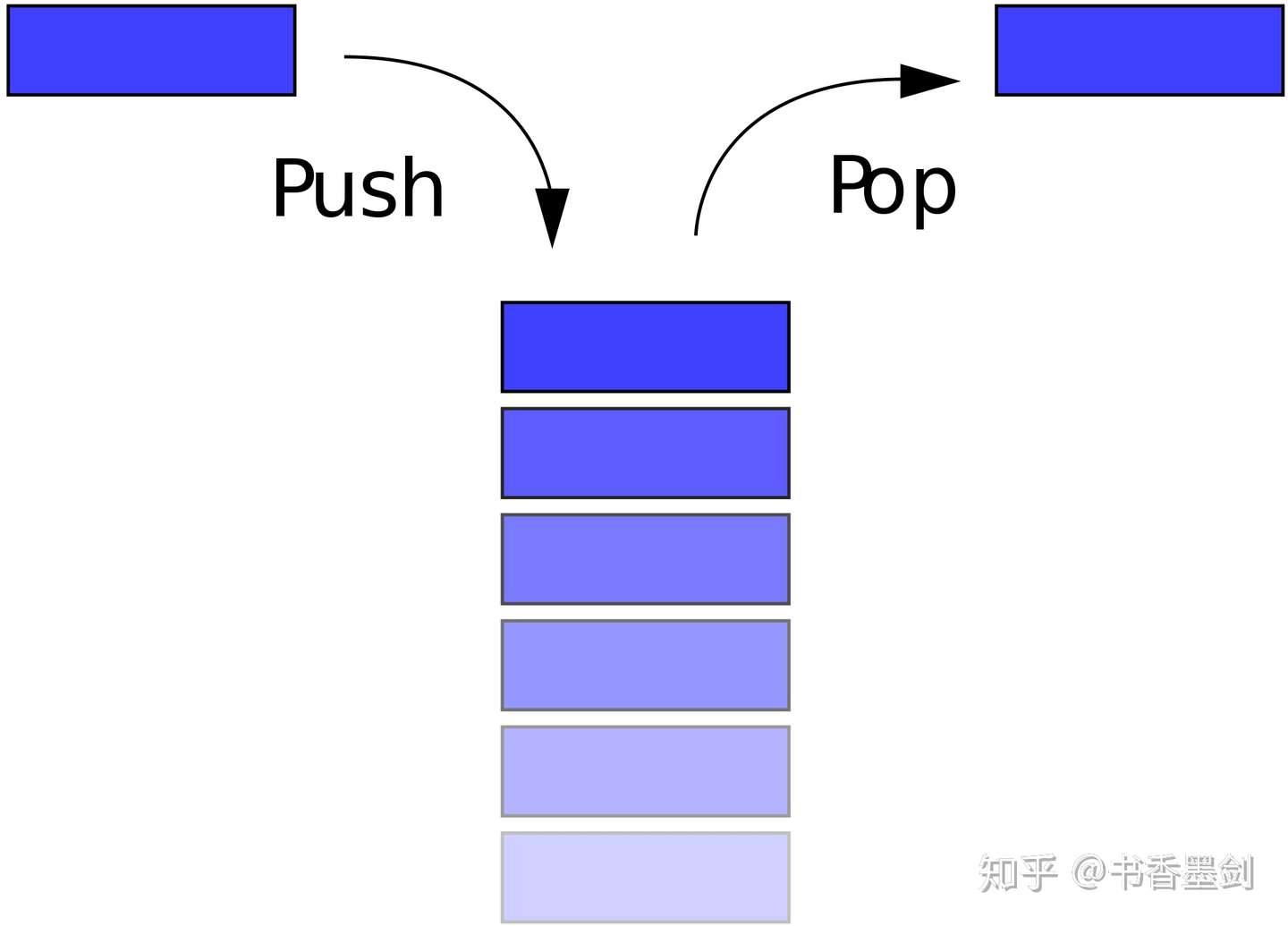
想象栈就是一摞盘子,你只能在最上面放盘子或者拿走盘子。对应起来,栈的操作就有两个:
- push 操作,往栈顶放入一个数据。
- pop 操作,从栈顶取走一个数据。
解题思路
回到这道题目,一开始看起来题目有点绕,让人不知道要做什么。后来 Helen 提议,既然题目要求是考虑在最初空栈上进行的推入 push 和弹出 pop 操作,那么我们不妨就建立一个空栈尝试用程序的方式来模拟一遍操作的流程,看看会不会明朗点:
function validateStackSequences(pushed, popped) {
const stack = [];
pushed.forEach(ele => {
stack.push(ele);
stack.pop();
});
return !stack.length;
}这样我们就建立了一个栈,并且在按题目中 pushed 数组的顺序将元素 push 进栈, 然后再按照同样的顺序 pop 出去。
不过这样子就跟数学题里面一边放水,一边加水的疯狂管理员一般,返回的结果肯定为 true。
回头再看看题目,发现其实就是在这个一边增加一边移出的过程上,添加了一个条件:只能按照 poped 的顺序来 pop 数据,看看能不能将 stack 清空 。
再拆解一下目标,就更明确了:
- 按照
pushed的顺序将元素push入栈。 - 在
push的过程中尝试pop元素。 pop元素的顺序要和poped的顺序一样。
要满足这三个条件,一个方法就是,尝试在 push 的每一步时,尽可能按照指定顺序 pop 出所有的元素。根据这个思路,Helen 给出了题解:
function validateStackSequences(pushed, popped) {
const stack = [];
let popIndex = 0;
for (const val of pushed) {
stack.push(val);
while (stack.length !== 0 && stack[stack.length - 1] === popped[popIndex]) {
stack.pop();
popIndex++;
}
}
return stack.length === 0;
}书香的思路一模一样,只是把代码写的更短了点 :
function validateStackSequences(pushed, popped) {
const stack = [];
pushed.forEach(ele => {
stack.push(ele);
while (stack.length && stack[stack.length - 1] === popped[0]) {
stack.pop();
popped.shift();
}
});
return !stack.length;
}Extra Go
对于书香和 Helen 这样的初级选手,通过实现一个栈结构来模拟题目中要求的操作,解出题目,就已经开心地到一边去玩耍了 ~
但对于追求完美的曾大师来说,push 和 pop 这两个操作,都非常消耗计算资源。而这种把数据一边 push 一边 pop 的疯狂操作显然是不能容忍的。
为此,他写出了 2 米长的 Go 语言代码:
func validateStackSequences(pushed []int, popped []int) bool {
if len(popped) == 0 {
return true
}
pushedValues := make(map[int]int) //存储所有的已经入栈的值和数组索引
left := 0
right := 0
for i := 0; i < len(pushed); i++ {
if pushed[i] == popped[0] {
pushed[i] = -1 // 出栈
left = i-1
right = i+1
break
} else {
pushedValues[pushed[i]] = i
}
}
for j := 1; j < len(popped); j++ {
if _, ok := pushedValues[popped[j]]; ok { // 值已经加入stack了
for left >= 0 {
if pushed[left] == -1 {
left--
} else {
break
}
}
if left < 0 {
left = 0
}
if popped[j] != pushed[left] {
return false
} else { // 值相等,出栈
pushed[left] = -1
left--
}
} else { // 值没有加入stack,继续往前找
for right < len(popped) {
if popped[j] == pushed[right] { // 找到了
pushed[right] = -1 //出栈
left = right - 1 // 重新赋值left
right ++ // 重新赋值right
break
} else { // 没有找到,继续往前
pushedValues[pushed[right]] = right
right++
}
}
}
}
return true
}嗯…… 8 ms 的运行时间……

贪心算法
不知道你有没有发现,这道题目,在开始的时候看起来比较绕,但是真正实现起来并没有那么困难?
其实关键点在于 「分而治之」,将任务中的每一步拆分开来,并且在每一步时,都尽可能去寻找最优解,再将每一步的最优解达到合起来,看是否能达成目标。
这种思路的算法就称为 「贪心算法」,它在遇到寻找最优解问题的情况下,能够提供很大的帮助。
下次见~





