
ALU 介绍
上次我们讲到了计算机如何表示和存储数字以及文字,但计算机真正的目标是进行计算、有意义地处理数字,比如把两个数字相加等等。这些事是由计算机的一个叫“算术逻辑单元(ALU)”的部件来处理的。ALU 是计算机的大脑,也是现代计算机的基石,基本上计算机所有的操作运算都会用到它。
ALU 有 2 单元,1 个算术单元,1 个逻辑单元,所以接下来分两块来分别介绍它们。

算术单元
算数单元负责计算机里所有的数字操作,比如加减法等等。要完成“将两个数相加”这个操作,需要制造出新的部件“加法器”,我们会用之前抽象出的“逻辑门” —— 与门、或门、非门、异或门 —— 来进行更高层次地抽象,组装成我们想要的部件!
半加器
最简单的加法电路,就是拿两个比特(0 或 1)加在一起。它会有 2 个输入,以及 1 个输出:两个输入数字的和。
我们的输入和输出都只有 1 个比特,所以会有以下几种情形出现:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 0
- 1 + 1 = 2 = 10(二进制)
注意,在二进制里没有 2 这个数字,计算出来的结果需要进位,表示为 10。发现了什么?这 4 个加法结果的末尾和之前讲的“异或门”的输入输出结果一模一样!于是我们放上一个异或门:
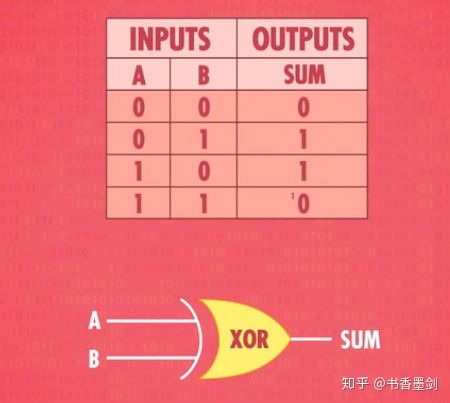
但我们 1 + 1 这个运算的结果是 10,有一个“进位”上的数字被置为了 1,所以我们可以用之前的“与门”加入一条“进位”输出电路,来保存这个进位:
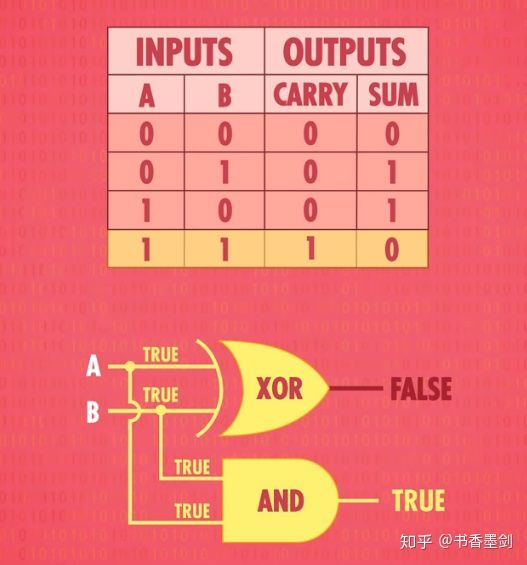
我们就制造出了一个“半加器”,把它进行抽象,加入我们的工具箱:
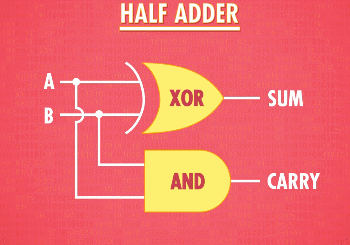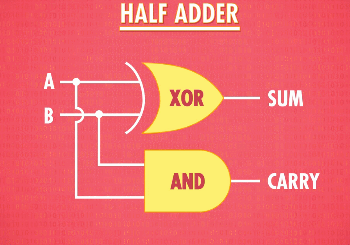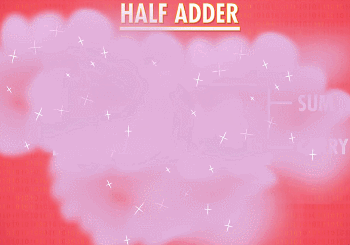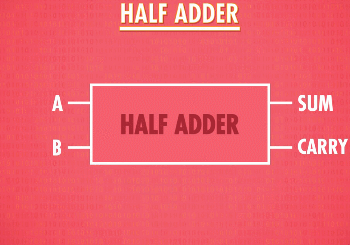
全加器
半加器只能计算 1 位二进制的运算,如果超过了 1 位,我们就需要“全加器”。想一想我们之前的二进制计算,半加器相加后可能产生进位,那之后每一位的计算可能就会有 2 个对应位的数字加上“进位”的数字。因此,我们的全加器就会有 3 个输入,以及 2 个输出,它的可能性也多了许多:
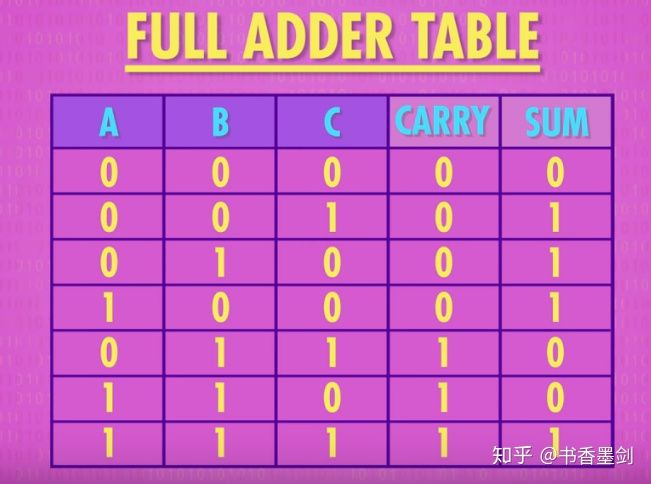
我们可以利用半加器来做制作全加器,首先用一个半加器将两位数字相加,再把“进位”的数字输入另一个半加器,与前一个半加器输出的“和”进行运算,最后再用一个“或门”来监测是否有新的“进位”:
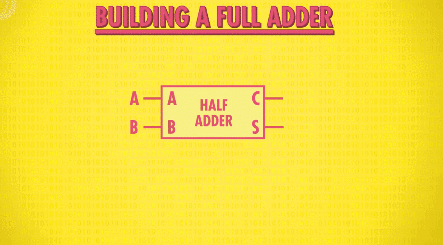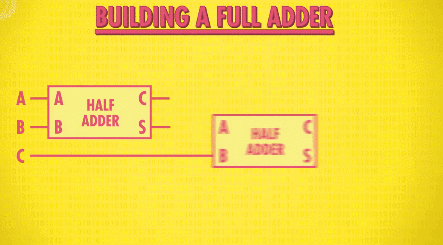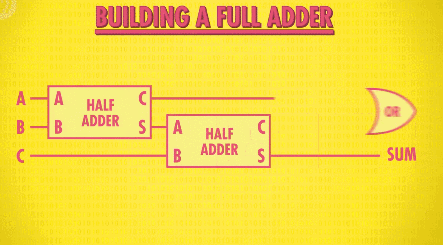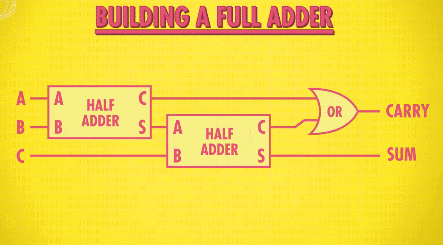
这样就制造出了全加器!同样我们把它抽象,加入工具箱:
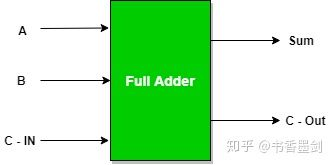
8 位二进制加法器
接下来,让我们看看怎么制作一个 8 位的加法器。假设我们要把两个名字为数字“A”和数字“B”的 8 位二进制的数相加。
首先,我们需要一个半加器把这连个数字的最右边一位“A0”和“B0”加起来,得到一个“和”输出和一个“进位”输出。
然后下一位的数字“A1”和“B1”除了对应相加,还要加上前一位的“进位”输出,因此我们连上一个全加器,同样得到了“和”与“进位”的输出。
再将上一步的“进位”输出连入下一个全加器就可以计算下一位数字了,以此类推,就可以制造出 8 位二进制的加法器了:
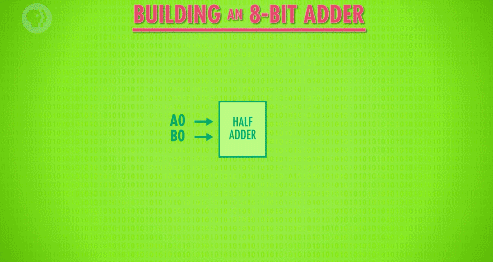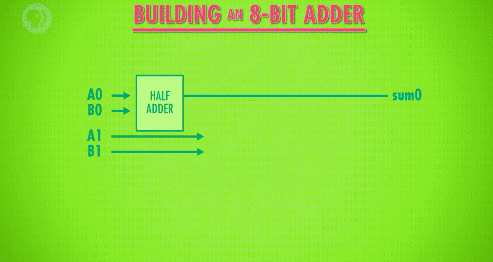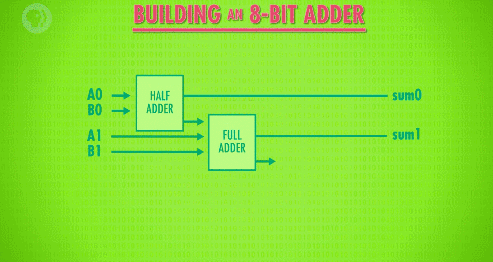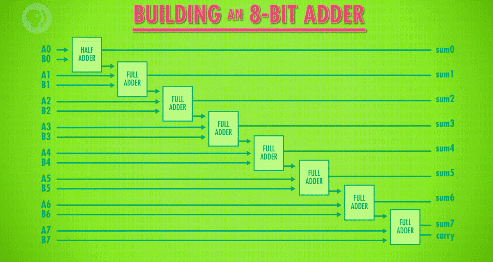
注意,我们最后一位的数字计算是有“进位”的,如果两个相加的数过大,在这里产生了进位,结果超出了 8 位,这就叫做“溢出 (overflow)”。
溢出意味着结果超出了对应位数可以表示的数字,这会导致错误和不可预期的结果。例如以前在 8 位机上玩“吃豆人”的时候,如果你玩到了第 256 关(8 位二进制最多可以表达 0~255),那屏幕上就会出现乱码,游戏就会出错:

为了避免“溢出”,我们可以加更多的全加器来制造 16 位、32 位、甚至 64 位的加法器。代价就是需要更多的逻辑门部件来制造,并且每次进位会花一些更多的时间。
其他操作
另外,除了加法,算术单元也可以进行其他的运算,大概有一下这些:
- 加法(ADD)
- 减法(SUBTRACT)
- 增量+1(INCREMENT)
- 减量-1(DECREMENT)
不同的计算也跟加法器类似,是用不同的逻辑门组合出来的。但是在其中并没有乘法或除法,因为简单的 ALU 中并没有专门的器件来处理这两个运算,而是通过重复多次的加法或减法来完成的,例如:
12 × 5 = 12 + 12 + 12 + 12 + 12
但是现代计算机、智能手机等更好的处理器中,为了速度更快,也加入了乘法和除法的运算单元。它们更复杂一些,但也是通过更多个逻辑门的各种组合来实现的!
逻辑单元
顾名思义,逻辑单元在计算机内负责执行逻辑操作。比如之前说的“与”、“或”、“非”、“异或”。另外,它还能做简单的数值测试,比如利用许多个“或门”,来检测一个 8 位数字是否为“0”:
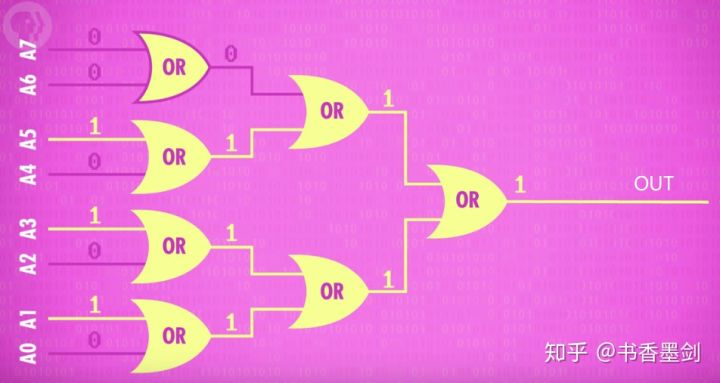
ALU 抽象
利用大量逻辑门的组合,我们可以构建出一个 ALU。回到一开始提到的英特尔 74181,它只能处理 4 位输入,并且不能直接进行乘除法的计算。即便如此,要构建出它,也用了 70 个逻辑门:
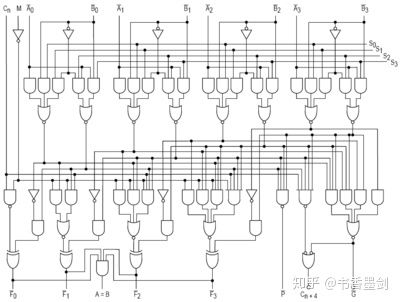
仅仅 4 位的 ALU 已经如此复杂了,而 8 位的 ALU 更是需要几百个逻辑门,因此工程师们在使用 ALU 的时候,将它抽象成了一个符号:
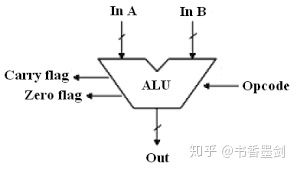
它接受两个操作数输入(InA,InB),以及 1 个表示要进行的是哪个运算的操作代码 (Opcode),然后输出一个结果 (Out)。
另外 ALU 还会有各种标志位 (flag),来表示计算的状态。例如: 进位标志 (Carry flag) 表示这次计算有没有进位,0 标志 (Zero flag) 表示这次计算的结果是不是为 0,这样就可以方便地判断计算是否溢出,或者两个输入的数是否相等。高级的 ALU 中,会有更多的标志位,可以帮助处理器更快更方便地运算。
之后
目前为止,我们了解了电子计算机是如何在没有齿轮的情况下进行计算的了。接下来,我们会利用 ALU 来制造计算的 CPU(中央处理器),越来越接近我们现在的计算机了!下次见~





